του Γιώργου Μπαντέ
του Γιώργου Μπαντέ
ΤΑ ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΤΗΣ ΜΑΘΗΜΑΤΙΚΗΣ ΙΣΤΟΡΙΑΣ
Τα μαθηματικά κουβαλούν από τη γέννα τους την αφαίρεση της φαντασίας. Για τους Έλληνες φιλοσόφους που διαμόρφωναν και καθοδηγούσαν τους μαθηματικούς, τα μαθηματικά θα πρέπει να είναι ένα σύνολο από λογικούς συλλογισμούς της διάνοιας·, ώστε να φτάσουν σε αλήθειες για τα φυσικά φαινόμενα. Η πρώτη αρχή λοιπόν είναι ότι τα μαθηματικά ασχολούνται με αφαιρέσεις αφού για τον Αριστοτέλη και τους εμπειρικούς φιλοσόφους τα μαθηματικά αντικείμενα είναι αποτέλεσμα αφαιρετικής διαδικασίας, που συμβαίνει στο μυαλό μας, η οποία δεν συνεπάγεται αναγκαστικά και την ύπαρξη ενός
σύμπαντος Ιδεών όπως ο ιδεατός κόσμος του Πλάτωνα. Για την κατανόηση των Μαθηματικών απαιτείται φαντασία και αφαιρετική ικανότητα.
Ένας άλλος λόγος αυτής της αφαιρετικής άποψης είναι (Klein): αφού τα μαθηματικά έπρεπε να είναι αποτελεσματικά στη μελέτη τον φυσικού κόσμου θα έπρεπε να αγκάλιάσουν με μια αφηρημένη έννοια τα ουσιαστικά χαρακτηριστικά όλων των φυσικών περιστατικών π.χ θα έπρεπε η μαθηματική ευθεία γραμμή να περιγράφει μια τεντωμένη κλωστή, τις άκρες του χάρακα και τι τροχιές των φωτεινών ακτινών. Άρα η μαθηματική ευθεία δεν θα είχε πάχος, χρώμα, μοριακή δομή ή τάσεις. Έτσι οι Έλληνες ήταν ρητά ισχυριζόμενοι ότι τα μαθηματικά τους ασχολούνται με αφαιρέσεις όπως σημείο, γραμμή, ακέραιοι αριθμοί.
Υπάρχει όμως και η άλλη λειτουργία , αυτή της διαίσθησης, για την οποία ο Πουανκαρέ γράφει ότι «οι διαισθητικές έννοιες είναι το εργαλείο της επινόησης». Διαίσθηση, προαίσθηση, είναι η ικανότητα να καταλαβαίνουμε κάτι ενστικτωδώς, χωρίς να χρειάζεται συνειδητή συλλογιστική, είναι η ικανότητα απόκτησης γνώσης χωρίς τεκμήρια ή/και τη χρήση του λόγου. “( Oxford dictionary)
γράφει ότι «οι διαισθητικές έννοιες είναι το εργαλείο της επινόησης». Διαίσθηση, προαίσθηση, είναι η ικανότητα να καταλαβαίνουμε κάτι ενστικτωδώς, χωρίς να χρειάζεται συνειδητή συλλογιστική, είναι η ικανότητα απόκτησης γνώσης χωρίς τεκμήρια ή/και τη χρήση του λόγου. “( Oxford dictionary)
π.χ’θα επιτρέψουμε στη διαίσθησή μας να μας καθοδηγήσει.
Μέσα από αυτές τις έννοιες, η αρχή της νέας εποχής ήταν η αμφισβήτηση της γεωμετρικής διαίσθησης υπέρ της αφαίρεσης. Μια κλασσική περιγραφή μεταξύ διαίσθησης και αφαίρεσης είναι το αξίωμα της παραλληλίας του Ευκλείδη, η μοναδική παράλληλη προς ευθεία από σημείο εκτός, ήταν τόσο ισχυρή διαισθητικά που ήταν αξεπέραστη επί είκοσι αιώνες. Με την αντικατάστασή του από αυτό του Λομπατσέφσκυ, αυτό των δύο παραλλήλων μία προς κάθε κατεύθυνση, η γεωμετρία του έγινε πολύπλοκη και ακατανόητη όπως ένας σουρεαλιστικός πίνακας, αποκάλυψε έναν περίεργο κόσμο που εκ κατασκευής φαίνεται φανταστικός. Ο ίδιος ονόμασε τη γεωμετρία του φανταστική. Όμως ήταν συλλογιστικά έγκυρος, τα θεωρήματα προέκυπταν από τα αξιώματα μέσα από τον παραγωγικό συλλογισμό. Η νέα παραλληλία παραμόρφωσε την Ευκλείδεια ευθεία και το Ευκλείδειο επίπεδο, όπου οι γεωδαισιακές του, οι ευθείες Λομπατσέφσκυ, ήταν απροσπέλαστες από τη διαίσθηση και αφηρημένες.
Στην εξέλιξη των αριθμών που συμβαδίζει με την εξέλιξη των θεμελίων των μαθηματικών, βλέπει κανείς την ίδια σαφή πορεία προς την αύξηση της αφαίρεσης, εις βάρος της διαίσθησης, οι αριθμοί παρακολουθούν την εξέλιξη των μαθηματικών εννοιών.

Το πρώτο πράγματι χτύπημα της διαίσθησης ήταν στην Ελληνική αρχαιότητα, ήταν τα ασύμμετρα γεωμετρικά μεγέθη του ίδιου είδους. Δύο ευθύγραμμα τμήματα δεν μπορούσαν πάντα να μετρηθούν με ένα κοινό μέτρο! Δύο κόσμοι στις μετρήσεις, χρειάζονταν μια νέα αφαίρεση στους αριθμούς, ισχυρότερη από αυτή που συνέβη κατά την καταμέτρηση των προβάτων. Τώρα υπάρχουν κάποιοι αριθμοί, όχι σαν αυτούς που μετρούσαν τα μήλα ή τα κομμάτια τους που μας έδινε η διαίσθηση και η κοινή εμπειρία! Ήταν τόσο πολύπλοκο ώστε οι Έλληνες το ξεπέρασαν μέσω της γεωμετρίας. Αργότερα έχουμε ακόμα μεγαλύτερη αφαίρεση, όταν με τη συμβολική άλγεβρα του Peacock, οι αριθμοί έγιναν σύμβολα, συμβολική αφαίρεση, αρνητικοί αριθμοί και σιγά- σιγά η αφηρημένη άλγεβρα άρχισε να μελετάει δομές που το νόημα το έπαιρναν εκ των υστέρων.
Όλα τα μαθηματικά φαίνονταν να είναι εξαγωγή θεωρημάτων με λογική αυστηρότητα από αξιωματικοποιημένες παραδοχές, αλλά η αλήθεια των αξιωμάτων δεν ήταν εξασφαλισμένη από τη διαίσθηση παρά μόνο από αφαιρετικές θεωρήσεις.. Η διαίσθηση άρχισε να γίνεται πηγή παραδόξων·, οπότε η λογική αυστηρότητα έλυνε τα προβλήματα εις βάρος της διαίσθησης. Όλη η αξιωματική κίνηση των σύγχρονων μαθηματικών στοχεύει στον περιορισμό της διαίσθησης από την αφαίρεση της λογικής συλλογιστικής.
τα καθαρά μαθηματικά, η γενίκευση
Μετά την εισαγωγή των τετραδονίων από το Χάμιλτον, για τα οποία ο ίδιος είχε στο μυαλό του φυσικές εφαρμογές, άλλοι μαθηματικοί αναγνωρίζοντας ότι θα μπορούσαν να υπάρχουν πολλές άλγεβρες, ανέλαβαν να διερευνήσουν όλες τις δυνατές άλγεβρες, έχοντας ή όχι οποιαδήποτε δυνατότητα εφαρμογής. Έτσι γεννιούνται τα καθαρά μαθηματικά.
Τα καθαρά μαθηματικά είναι η μελέτη των μαθηματικών εννοιών ανεξάρτητα από οποιαδήποτε εφαρμογή εκτός των μαθηματικών. Αυτές οι έννοιες μπορεί να προέρχονται από πραγματικές ανησυχίες, και τα αποτελέσματα που λαμβάνονται μπορεί αργότερα να αποδειχθούν χρήσιμα για πρακτικές εφαρμογές, αλλά οι καθαροί μαθηματικοί δεν βασίζονται κυρίως σε τέτοιες εφαρμογές. Αντίθετα, η έκκληση αποδίδεται στην πνευματική πρόκληση και την αισθητική ομορφιά της επεξεργασίας των λογικών συνεπειών των βασικών αρχών.
οποιαδήποτε εφαρμογή εκτός των μαθηματικών. Αυτές οι έννοιες μπορεί να προέρχονται από πραγματικές ανησυχίες, και τα αποτελέσματα που λαμβάνονται μπορεί αργότερα να αποδειχθούν χρήσιμα για πρακτικές εφαρμογές, αλλά οι καθαροί μαθηματικοί δεν βασίζονται κυρίως σε τέτοιες εφαρμογές. Αντίθετα, η έκκληση αποδίδεται στην πνευματική πρόκληση και την αισθητική ομορφιά της επεξεργασίας των λογικών συνεπειών των βασικών αρχών.
Ένα παράδειγμα καθαρών μαθηματικών είναι η αφηρημένη άλγεβρα.
Η αφηρημένη άλγεβρα εμφανίστηκε στις αρχές του 20ού αιώνα, με το όνομα σύγχρονη άλγεβρα. Η μελέτη της ήταν μέρος της προσπάθειας για περισσότερη πνευματική απόλαυση και λογική αυστηρότητα στα μαθηματικά.
Αρχικά, οι παραδοχές στην κλασική άλγεβρα, από τις οποίες εξαρτώνταιτο σύνολο των μαθηματικών (και τα κύρια μέρη των φυσικών επιστημών), πήραν τη μορφή αξιωματικών συστημάτων. Το αποτέλεσμα της αφαίρεσης στα καθαρά μαθηματικά είναι ότι αποκαλύπτει βαθιές συνδέσεις μεταξύ διαφορετικών τομέων, όπως φαίνεται π.χ στις δομές της αφηρημένης άλγεβρας, για παράδειγμα το σύνολο των ακεραίων Ζ, των ρητών Q, των πραγματικών R των μιγαδικών C με την αφαίρεση των συνήθων πράξεων της πρόσθεσης και του πολλαπλασιαμου είναι αντιμεταθετικοί δακτύλιοι με μονάδα. Τώρα οι αριθμοί βασίζονται σε μια πλήρη δήλωση του σώματος των νόμων και των αξιωμάτων που υπαγορεύουν τις λειτουργίες (πράξεις) που χρησιμοποιούνται. Οι πράξεις αυτές καθορίζουν τους αριθμούς κι όχι οι αριθμοί τις πράξεις, έχουμε τη μετάβαση από τη διαίσθηση στη λογική αφαίρεση. Αυτή η κατεύθυνση στη μελέτη των αριθμητικών συστημάτων περιγράφεται στο βιβλίο μου «Γκαλουά η θεωρία των εξισώσεων ως θεωρία ομάδων»
 Οι μαθηματικοί όχι πλέον ικανοποιημένοι με τον καθορισμό ιδιοτήτων συγκεκριμένων αντικειμένων, άρχισαν να στρέφουν την προσοχή τους στη γενική θεωρία. Η κύρια κατεύθυνση των καθαρών μαθηματικών είναι κατεύθυνση της γενίκευσης, Η μελέτη των αριθμών, που ονομάζεται άλγεβρα στο προπτυχιακό επίπεδο, επεκτείνεται στην αφηρημένη άλγεβρα σε πιο προχωρημένο επίπεδο, και η μελέτη των συναρτήσεων, που ονομάζεται λογισμός στο επίπεδο του κολλεγίου γίνεται μαθηματική ανάλυση
Οι μαθηματικοί όχι πλέον ικανοποιημένοι με τον καθορισμό ιδιοτήτων συγκεκριμένων αντικειμένων, άρχισαν να στρέφουν την προσοχή τους στη γενική θεωρία. Η κύρια κατεύθυνση των καθαρών μαθηματικών είναι κατεύθυνση της γενίκευσης, Η μελέτη των αριθμών, που ονομάζεται άλγεβρα στο προπτυχιακό επίπεδο, επεκτείνεται στην αφηρημένη άλγεβρα σε πιο προχωρημένο επίπεδο, και η μελέτη των συναρτήσεων, που ονομάζεται λογισμός στο επίπεδο του κολλεγίου γίνεται μαθηματική ανάλυση
και συναρτησιακή ανάλυση σε πιο προχωρημένο επίπεδο.
Μια γενίκευση είναι μια μορφή αφαίρεσης με την οποία κοινές ιδιότητες συγκεκριμένων περιπτώσεων διατυπώνονται ως γενικές έννοιες ή αξιώσεις. Π.χ. μια απλή γενίκευση είναι η επέκταση της σειράς MacLaurin σε σειρά Taylor, και η επέκταση του τύπου (l+x)v στο διωνυμικό τύπο
(χ+t)’1·
Το νόημα του αξιωματικού συστήματος είναι ακριβώς γενίκευση δια της αφαίρεσης. Τα καθαρά μαθηματικά συχνά δείχνουν μια τάση για αυξημένη γενίκευση. Η γενίκευση των θεωρημάτων ή των μαθηματικών δομών μπορεί να οδηγήσει σε βαθύτερη κατανόηση των αρχικών θεωρημάτων ή δομών. Ως πρωταρχικό παράδειγμα γενίκευσης, το πρόγραμμα Erlangen του 1872, περιελάμβανε επέκταση της γεωμετρίας για να φιλοξενήσει γεωμετρίες εκτός Ευκλείδειας, όπου η γεωμετρία ορίζεται ως μια αναλλοίωτη θεωρία μιας ομάδας
μετασχηματισμών. (https://0p0po
www.academia.edu/28663551/) Ακόμα οι κωνικές τομές -έλλειψη, παραβολή υπερβολή-
αντιπροσωπεύονται αλγεβρικά, από εξισώσεις δεύτερου βαθμού. Μερικές καμπύλες που αντιπροσωπεύονται από εξισώσεις τρίτου βαθμού είναι χρήσιμες σε εφαρμογές. Η γενίκευση μεταπηδάει σε καμπύλες που οι εξισώσεις τους είναι ν-βαθμού και μελετάει τις ιδιότητές τους με λεπτομέρειες χωρίς καμιά από αυτές να εμφανίζεται σε φυσικά φαινόμενα.
ΕΙΣΑΓΩΓΗ
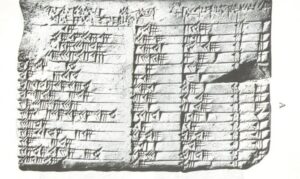
Τι είναι οι αριθμοί; πότε εμφανίστηκαν; είναι τα είδωλα της πραγματικότητας στη αντίληψη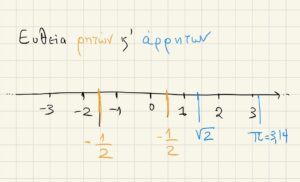 ή η ίδια η πραγματικότητα όπως έλεγαν οι Πυθαγόρειοι; Ο Πλάτων ισχυρίστηκε ότι οι αριθμοί υπάρχουν σε κάποιο αφηρημένο παράδεισο ανεξάρτητο από το μυαλό. Οι νομιναλιστές (Μπαμπινιώτης) ισχυρίζονται ότι δεν υπάρχει τέτοιος παράδεισος. Σαφώς, δεν μπορούμε να δούμε, να ακούσουμε, να γευτούμε ή να νιώσουμε αριθμούς. Αλλά αν δεν υπάρχουν αριθμοί, τι είναι τα μαθηματικά; Χιλιάδες χρόνια π.Χ. οι Βαβυλώνιοι επιστήμονες χρησιμοποίησαν έξυπνες αριθμητικές σημειώσεις να συνθέσουν αστρονομικούς πίνακες εκπληκτικής ακρίβειας. Δεκάδες χιλιάδες χρόνια πριν απ’ αυτούς, οι Νεολιθικοί πρόγονοί μας περιέγραψαν τους πρώτους γραπτούς αριθμούς με χάραξη οστών ή με ζωγραφική κουκκίδων, σε τοίχους σπηλαίων.(Stanislas Dehaene, Oxford Unuversity Press)
ή η ίδια η πραγματικότητα όπως έλεγαν οι Πυθαγόρειοι; Ο Πλάτων ισχυρίστηκε ότι οι αριθμοί υπάρχουν σε κάποιο αφηρημένο παράδεισο ανεξάρτητο από το μυαλό. Οι νομιναλιστές (Μπαμπινιώτης) ισχυρίζονται ότι δεν υπάρχει τέτοιος παράδεισος. Σαφώς, δεν μπορούμε να δούμε, να ακούσουμε, να γευτούμε ή να νιώσουμε αριθμούς. Αλλά αν δεν υπάρχουν αριθμοί, τι είναι τα μαθηματικά; Χιλιάδες χρόνια π.Χ. οι Βαβυλώνιοι επιστήμονες χρησιμοποίησαν έξυπνες αριθμητικές σημειώσεις να συνθέσουν αστρονομικούς πίνακες εκπληκτικής ακρίβειας. Δεκάδες χιλιάδες χρόνια πριν απ’ αυτούς, οι Νεολιθικοί πρόγονοί μας περιέγραψαν τους πρώτους γραπτούς αριθμούς με χάραξη οστών ή με ζωγραφική κουκκίδων, σε τοίχους σπηλαίων.(Stanislas Dehaene, Oxford Unuversity Press)
Ο Γκάους μας προετοιμάζει για το φαινόμενο των αριθμών στα μαθηματικά, ως εξής:
«Η αλήθεια βρίσκεται στον αριθμό, ο οποίος είναι η βάση της αριθμητικής, της άλγεβρας, του λογισμού και των υψηλότερων κλάδων της ανάλυσης, οι οποίοι θεμελιώνονται στην αριθμητική, γιατί οι αλήθειες της αριθμητικής είναι καθαρές στο μυαλό μας., σύμφωνα την πιο ειλικρινή μου πεποίθηση η θεωρία του χώρου κατέχει μια εντελώς διαφορετική θέση στη γνώση από αυτή των καθαρών μαθηματικών [τα μαθηματικά που θεμελιώνονται στους αριθμούς ] … .αν ο αριθμός είναι αποκλειστικά το προϊόν του μυαλού μας, ο χώρος έχει μια πραγματικότητα έξω από το νου και δεν μπορούμε πλήρως να περιγράφουμε τους νόμους του,.,.Γκάους»
Πράγματι η δημοσίευση του Ρήμαν του 1854 έπεισε πολλούς μαθηματικούς ότι μια μη Ευκλείδεια γεωμετρία θα μπορούσε να είναι η γεωμετρία του φυσικού χώρου, και δεν μπορούσαν να είναι βέβαιοι ποια γεωμετρία ήταν αληθής. Τώρα έχουμε
ο θεός αεί αριθμητικοποιεί…. J. Jacobi απέναντι στο
θεός αεί γεωμετρεί όπως ισχυρίστηκε ο Πλάτων
Τι εννοεί ο Τκάους με τη λέξη αλήθεια; ποια αλήθεια; Οι περισσότεροι μαθηματικοί αναφέρονται στην αλήθεια των μαθηματικών και ασπάζονται την άποψη του Τκάους.
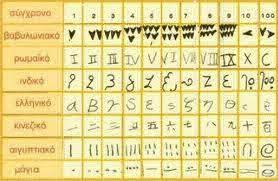 Η ιδέα αυτού του βιβλίου είναι στα πλαίσια των μαθηματικών, μαθηματική αλήθεια είναι η μαθηματική δηλαδή η λογική απόδειξη και μόνο, που παράγεται μέσα στο μυαλό και αν τα μαθηματικά είναι φανταστικά (fictions) τότε και οι αριθμοί είναι φανταστικοί, αφού φαίνεται ότι:
Η ιδέα αυτού του βιβλίου είναι στα πλαίσια των μαθηματικών, μαθηματική αλήθεια είναι η μαθηματική δηλαδή η λογική απόδειξη και μόνο, που παράγεται μέσα στο μυαλό και αν τα μαθηματικά είναι φανταστικά (fictions) τότε και οι αριθμοί είναι φανταστικοί, αφού φαίνεται ότι:
Οι αριθμοί είναι η πρώτη ύλη για τις εξελίξεις στα μαθηματικά.
Κάθε επανάσταση στα μαθηματικά συνδέεται με νέους αριθμούς, δηλαδή με νέες μετρήσεις όπως
συμβολική άλγεβρα ~ αρνητικοί αριθμοί άλγεβρα Χάμιλτον ~ τετραδόνια- μέτρηση των περιστροφών στο χώρο
λογισμός ~ απειροστά-μέτρηση των απειροελάχιστων μεγεθών
σύνολα του Κάντορ ~ υπερπεπερασμένοι αριθμοί-μέτρηση του απείρου
άρρητοι ~ συνεχές των πραγματικών αριθμών- μετρήσεις στους πραγματικούς αριθμούς κ.λ.π
«σήμερα τα μαθηματικά, όπως λέμε έχουν
αριθμητικοποιηθεί… Πουανκαρέ Παρίσι 1900 δεύτερο παγκόσμιο μαθηματικό συνέδριο».
και όλα αυτά σημαίνουν ότι χωρίς μετρήσεις δεν υπάρχουν μαθηματικά και χωρίς αριθμούς δεν υπάρχουν μετρήσεις.
Το βιβλίο αυτό γράφτηκε σε προπτυχιακό επίπεδο, είναι μια προσιτή έρευνα για το πώς η έννοια των αριθμών και των αριθμητικών συστημάτων1 έχει εξελιχθεί από την επιστημονική επανάσταση στα τέλη του 16ου αιώνα στη Δυτική Ευρώπη, μέχρι τον ορισμό των πραγματικών αριθμών από τον Dedekind έως τους υπερπεπερασμένους (transfinite) αριθμούς του Cantor, ακόμα και στους υπερπραγματικούς αριθμούς του Robinson (ΠΑΡΑΡΤΗΜΑ)
Οι αριθμοί είναι τα γνωστικά εργαλεία των μετρήσεων και ως εργαλεία έχουν διαμορφωθεί σύμφωνα με τα μετρούμενα μεγέθη., άλλοι αριθμοί μετρούν αδιαίρετα μεγέθη (πρόβατα), άλλοι, τα μεγέθη που διαιρούνται σε ίσα μέρη, άλλοι μεγέθη που είναι μόνο προσεγγίσιμα, τα τετραδόνια μετρούν τις περιστροφές στο χώρο, άλλοι μετρούν το άπειρο κλπ. όμως το όχημα της επέκτασης των αριθμητικών συστημάτων ήταν η επέκταση της άλγεβρας πέρα από την απλή επίλυση των εξισώσεων, οι οποίες απαιτούσαν αφηρημένη λογική θεμελίωση των αριθμητικών συστημάτων που ήταν ο σύνδεσμος ανάμεσα στους αριθμούς και στην άλγεβρα.
1 Οι αριθμοί μπορούν να ταξινομηθούν σε σύνολα, που ονομάζονται αριθμητικά συστήματα.
Είναι γιατί, οι αριθμοί είναι σύμβολα του νου, υπάρχουν μόνο στο μυαλό μας, και ως εκ τούτου μπορούν να περιγράφουν πράγματα της φαντασίας μας, μακριά από οποιαδήποτε διαίσθηση, όπως στις μη Ευκλείδειες ευθείες γραμμές. Τα μαθηματικά δεν είναι πειράματα της φυσικής, τα μαθηματικά ζουν στη μαθηματική φαντασία, οι αριθμοί φέρνουν την αφαίρεση μέσα τους. Η πρώτη συστηματική μελέτη των αριθμών ως αφαιρέσεις (δηλαδή, ως
αφηρημένες οντότητες), συνήθως πιστώνεται στους αρχαίους Έλληνες φιλόσοφους στον ΕΙυθαγόρα και στον Αρχιμήδη. Στα στοιχεία του Ευκλείδη συναντούμε τον πρώτο ορισμό των φυσικών αριθμών: «Μονάς έστιν, καθ’ ήν έκαστον των δντων εν λέγεται. Αριθμός δε το έκ μονάδων συγκείμενον πλήθος.» Ο Dedekind έλεγε ότι οι αριθμοί είναι μια ελεύθερη δημιουργία του ανθρώπινου μυαλού και ο Peacock ήταν ο πρώτος που προσπάθησε να εκφράσει τους αριθμούς ως τέτοιες δημιουργίες, και ουσιαστικά κινήθηκε προς αυτήν την κατεύθυνση. Με την απελευθέρωση των αριθμών από την πραγματικότητα απελευθέρωσε την άλγεβρα από την αριθμητική.
Οι αριθμοί σιγά-σιγά άρχισαν να εμφανίζονται ως οντότητες που ζούσαν ανεξάρτητα από αυτό που μετρήθηκε ή παρίσταναν . Αυτό συνεχίστηκε με το Χάμίλτον που όρισε μια νέα άλγεβρα, με τον Dedekind που στα τέλη του 19ου αιώνα άρχισε πραγματικά να σκέφτεται για τον ορισμό των αριθμών και των συστημάτων αριθμών μέσα από τον ορισμό ενός συνεχούς. Αργότερα ορίζει επίσης τους πραγματικούς με τις τομές του, γεμίζοντας την πραγματική γραμμή, για να σχηματίσει ένα συνεχές με στόχο την αυστηρή θεμελίωση των πραγματικών αριθμών..που είναι η αριθμητική βάση όλων των μαθηματικών. Στη μελέτη των μεταμαθηματικών για τη σχετική συνέπεια των αξιωματικών συστημάτων η συνέπεια πολλών κλάδων των μαθηματικών μπορεί να αναχθεί στη συνέπεια μερικών βασικών κλάδων, που για το μεγαλύτερο μέρος των μαθηματικών και για το σύνολο της φυσικής είναι το σύστημα των πραγματικών αριθμών.» (βιβλίο μου η σχετικότητα της γεωμετρίας και ο χώρος σελ.33 www.mpantes.gr)
 Αυτό συμπληρώνει τα αριθμητικά συστήματα που έχουμε συνηθίσει να τα χτίζουμε σε μια ωραία ιεραρχική δομή. Με το συνεχές των αριθμών, το απίθανο αυτό διαισθητικό παράδοξο, ένα πεπερασμένο διάστημα περιέχει τώρα απεριόριστα πολλούς πραγματικούς αριθμούς, όσους υπάρχουν σε ολόκληρη την πραγματική γραμμή. Αυτό οδήγησε τον Cantor να μελετήσει τους transfinite ordinals (υπερπεπερασμένους διατακτικούς αριθμούς)
Αυτό συμπληρώνει τα αριθμητικά συστήματα που έχουμε συνηθίσει να τα χτίζουμε σε μια ωραία ιεραρχική δομή. Με το συνεχές των αριθμών, το απίθανο αυτό διαισθητικό παράδοξο, ένα πεπερασμένο διάστημα περιέχει τώρα απεριόριστα πολλούς πραγματικούς αριθμούς, όσους υπάρχουν σε ολόκληρη την πραγματική γραμμή. Αυτό οδήγησε τον Cantor να μελετήσει τους transfinite ordinals (υπερπεπερασμένους διατακτικούς αριθμούς)
Τώρα αυτά τα σύμβολα (οι αριθμοί) βασίζονται σε μια πλήρη δήλωση του σώματος των νόμων και των αξιωμάτων που υπαγορεύουν τις λειτουργίες (πράξεις) που χρησιμοποιούνται στις μαθηματικές διαδικασίες.
Οι πράξεις αυτές καθορίζουν τους αριθμούς και όχι οι αριθμοί τις πράξεις
*Από το βιβλίο του Γιώργου Μπαντέ «η εξέλιξη των αριθμών στη μαθηματική ιστορία»
Ο Γιώργος Μπαντές κατάγεται από τον Πολύγυρο Χαλκιδικής και ζει στις Σέρρες. Σπούδασε μαθηματικά στο Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκς στα 1967-1971 και υπηρέτησε στ Δημόσια εκπαίδευση τριαντα δύο χρόνια.
Αρθρογραφεί στο: http://auth.academia.edu/GeorgeMpantes, και επίσης στο: https://www.scribd.com/user/46567432/George-Mpantes-MAthematics-teacher με επιπλέον αρκετές μεταφράσεις σημαντικών έργων μεγάλων διανοητών.
Έχει γράψει σειρά έντυπων & ηλεκτρονικών βιβλίων στα μαθηματικά(Τανυστικός λογισμός, Θεωρία Γκαλουά, κ.α.), και στη φυσική του ηλεκτρισμού και της σχετικότητας, (www.mpantes.gr) τα περισσότερα των οποίων εγκρίθηκαν και διατέθηκαν στις σχολικές βιβλιοθήκες και σε διάφορα Πανεπιστήμια της χώρας.