Η ΑΙΤΙΟΤΗΤΑ ΣΤΗ ΦΥΣΙΚΗ ΩΣ ΕΚΤΕΛΕΣΤΙΚΗ ΕΝΝΟΙΑ (μηχανική, κβαντομηχανική και χάος)

Γιώργος Μπαντές μαθηματικός www.mpantes.gr .

Η έννοια της αιτιότητας φιλοσοφική και επιστημονική .

Η διαφορική αιτιότητα του Νεύτωνα Ο νοητός «μηχανισμός» της διαφορικής αιτιότητας Ο ντετερμινισμός της κβαντικής μηχανικής Η πορεία του ντετερμινισμού , το χάος Μη γραμμικά συστήματα

Ένα μοντέλο χαοτικής συμπεριφοράς, επαναληπτικές συναρτήσεις Ντετερμινισμός και χάος

Περίληψη .

Ο χαρακτηρισμός μια θεωρίας ως ντετερμινιστικής, καθορίζεται από την προβλεψιμότητα που παράγει στα αποτελέσματα της θεωρίας.

Έχουμε διακρίνει τρεις περιοχές μετρήσεων με αντίστοιχες θεωρίες αιτιακής τάξης: (αιτιοκρατία, αβεβαιότητα, τυχαιότητα)

α. οι μετρήσεις στην περιοχή του μακροκόσμου που μας αποκαλύπτουν την αιτιοκρατική (ντετερμινιστική) τάξη αιτίας αποτελέσματος του Νεύτωνα, που ακόμα πιστεύεται ότι διέπει τον μακροσκοπικό κόσμο,

β. οι μετρήσεις στην περιοχή του μικρόκοσμου, όπου αναδεικνύεται η κβαντική τάξη του « όχι ακριβούς» , στατιστικού και απροσδιόριστου.

γ. οι μετρήσεις των επαναλήψεων στα μη-γραμμικά συστήματα και τη χαοτική μη-τάξη, δηλαδή τυχαιότητα που αποκαλύπτεται.

Προβλεψιμότητα είναι ο βαθμός πρόβλεψης ή πρόγνωσης που μπορούμε να έχουμε για την κατάσταση ενός συστήματος είτε ποιοτικά είτε ποσοτικά.

H έννοια της αιτιότητας , φιλοσοφική και επιστημονική .

Η βασική ιδέα για την έννοια της αιτιότητας, προέκυψε στο μυαλό μας από την άμεσα παρατηρούμενη κανονικότητα της φύσης . Ο ήλιος ανατέλλει κάθε

πρωί και δύει κάθε βράδυ, η διαδοχή των εποχών , η περιφορά των άστρων στον νυχτερινό ουρανό , ακόμα πιο περίπλοκες κινήσεις της σελήνης και των πλανητών, ήταν το έναυσμα για βαθύτερες παρατηρήσεις που δημιούργησαν βαθύτερες έννοιες. τον 6ο π.Χ. αιώνα στην Ιωνία αναπτύχθηκε ακριβώς η νέα αντίληψη, σύμφωνα με την οποία το Σύμπαν είναι κατανοητό, διότι έχει εσωτερική τάξη, διότι στη Φύση υπάρχουν κανονικότητες που επιτρέπουν την αποκάλυψη των μυστικών της και της λειτουργίας της. Η Φύση δεν είναι εντελώς απρόβλεπτη, διότι υπάρχουν κανόνες στους οποίους πρέπει να υπακούει. Σ’ αυτήν την τάξη και τον θαυμαστό χαρακτήρα του Σύμπαντος οι αρχαίοι έδωσαν το όνομα Κόσμος, δηλαδή ομορφιά (στολίδι). Νικόλαος Κ. Σπύρου καθηγητής του Τμήματος Φυσικής του Αριστοτελείου Πανεπιστημίου Θεσσαλονίκης.

Αυτή η έννοια του φυσικού νόμου μιας κανονικότητας εμπεριέχει το φιλοσοφικό δόγμα της αιτιοκρατίας:

Η αιτιοκρατία (ντετερμινισμός) (Determinism) είναι η φιλοσοφική τάση που επηρέασε ιδιαίτερα την επιστημονική σκέψη από την αρχαιότητα μέχρι και σήμερα. Αποδέχεται την ύπαρξη της αιτιότητας, την καθολική αιτιώδη και νομοτελειακή συνάφεια όλων των φαινόμενων στη φύση, μια γενική προβλεψιμότητα για το σύμπαν. (Θεοδωρίδης)

Δεμένη με αυτή την έννοια της αιτιοκρατίας είναι η έννοια της αιτίας:

…έννοια κάπως αόριστη και πολυσήμαντη . Στην πιο συνηθισμένη χρήση σημαίνει κάτι που παράγει ένα φαινόμενο ή μια αλλαγή, (παλιά ανθρωπομορφική άποψη, είτε ένα φαινόμενο που είναι σταθερά και αχώριστα δεμένο με ένα άλλο, ώστε άμα παρουσιαστεί αυτό, (η αιτία) να ακολουθεί κανονικά το άλλο (αποτέλεσμα, νεώτερη θετική και επιστημονική άποψη) ..Θεοδωρίδης

Δεν θα αναλύσω τη φιλοσοφική έννοια της αιτιότητας η οποία είναι αντιεπιστημονική και δεν προκύπτει από τη μεθοδολογία της επιστήμης

(άρθρο:       η μεθοδολογία της επιστήμης και η μεταφυσική                                      )

https://www.scribd.com/doc/260025743/),

αφού ψάχνοντας την αιτία της αιτίας ……………….. δεν θα καταλήξουμε πουθενά,

γνωρίζοντας (από τη μεθοδολογία της επιστήμης) ότι η ουσία του κόσμου πάντα μας διαφεύγει και ότι η δομή είναι μια δική μας κατασκευή. Η αιτία είναι ίδιου status με την ύλη του Αριστοτέλη, η βαθύτερη ουσία της ύλης δεν συλλαμβάνεται όπως και η βαθύτερη ουσία της αιτίας, είναι και τα δύο νοητικές μας κατασκευές που γεννήθηκαν

στην εμπειρία , καμωμένες για πρόχειρη ερμηνεία κι όχι για παραπάνω. Άλλωστε οι φιλοσοφικές εκδοχές αλλάζουν περίπου δύο φορές κάθε αιώνα.

Ο Ντέιβιντ Χιουμ αμφισβήτησε το φιλοσοφικό αυτό δόγμα της αιτιότητας. Σύμφωνα με τον Χιουμ, καμία αντίφαση δεν υπάρχει εάν ισχυριστεί κανείς για μια αιτία, ότι δεν συνεπάγεται το αποτέλεσμα που της αποδίδεται. Ούτε εμπειρικά είναι δυνατόν ποτέ να παρατηρήσουμε τον αιτιώδη δεσμό, την αναγκαία σχέση μεταξύ αιτίας και του αποτελέσματος. Απλώς, ό,τι στην πραγματικότητα παρατηρούμε σε μια αιτιώδη σχέση είναι το ένα γεγονός να διαδέχεται κάποιο άλλο γεγονός και τίποτε άλλο πέραν της χρονικής αυτής διαδοχής τους-«μετά τούτο, άρα εξαιτίας τούτου». Η αιτιατή σχέση και η εξάρτηση είναι λοιπόν πλάσμα                                                                  υποκειμενικό

r^pYOor.antichamletterhttp://ellimkahoaxes.gr…

Στο άρθρο αυτό, ακριβώς η κεντρική μας ιδέα είναι ότι διερευνούμε την αιτιότητα στη φυσική κι όχι στη φύση. Στη φύση βλέπουμε κανονικότητες και η μέθοδος να μελετήσουμε τις κανονικότητες , δηλαδή τις διαδοχές που λέει ο Hume, είναι νοητική. Ο ντετερμινισμός λοιπόν αποδίδεται στη φύση από το αξιωματικό μας σύστημα, το οποίο εγκαθιστούμε στα πράγματα κάνοντας επιστήμη. Όταν λέμε ότι ο κόσμος είναι ντετερμινιστικός θα εννοούμε ότι είναι προβλέψιμος κατ’ αρχήν, χωρίς να λαμβάνουμε υπ’ όψη τις πειραματικές ατέλειες ή το μεμονωμένο του συστήματος κλπ.

Η επιστημονική αιτιότητα είναι μια εκτελεστική έννοια που αναφέρεται στην προβλεψιμότητα της θεωρίας, είναι η εκτελεστική επιβεβαίωση των μαθηματικών αποτελεσμάτων της αντίστοιχης επιστημονικής θεωρίας η οποία συνδέει τα πράγματα. Η επιβεβαίωση είναι η επαλήθευση των προβλέψεων με τις πειραματικές μετρήσεις.

Ο πυρήνας λοιπόν της επιστημονικής αιτιότητας, είναι νοητικός,( η νόησή μας παράγει τον ντετερμινισμό) αλλά η αιτιότητα αναδεικνύεται από το πείραμα. Ο νοητικός μηχανισμός της αιτιότητας είναι η αξιωματική βάση και ο παραγωγικός συλλογισμός μέσα από το σχήμα

Προκείμενες ^ Αριστοτελική λογική ^ συμπέρασμα,

Άρθρο: Η αξιωματική μέθοδος Ευκλείδης Χίλμπερτ https://www.scribd.com/doc/161365902

που μεταφράζεται ανάλογα στις μεγάλες επιστημονικές θεωρίες της μηχανικής , της κβαντομηχανικής και της θεωρίας του χάους . Γιατί

«…φαίνεται πως η λογική επιβεβαιώνει τα φαινόμενα , και τα φαινόμενα το λογική, Αριστοτέλης», η γνωστή μας μετέπειτα εξέλιξη της σχέσης των μαθηματικών με την

πραγματικότητα. Η φράση αυτή εκφράζει μια από τις βαθύτερες κανονικότητες στη φύση (οι κρυμμένες κανονικότητες είναι ανώτερες από τις φανερές, Ηράκλειτος) και η συζήτηση γι’ απτή δεν έχει τελειώσει ακόμα.

Η εξέλιξη των έμβιων όντων δεν θα συνέβαινε αν δεν μπορούσαν να παρακολουθήσουν τις κανονικότητες στη φύση. Στους κατώτερους οργανισμούς αυτό μπορεί να συμβαίνει με απλές φωτοχημικές αντιδράσεις, αλλά στην ανθρώπινη εξέλιξη το μυστικό βρίσκεται στα «αναλυτικά ύστερα» του Αριστοτέλη.^[1]

Η Νευτώνεια αιτιότητα (διαφορική αιτιότητα) .

….. Η μηχανιστική άποψη φάνηκε πως θριαμβεύει ακόμα και

στις απόκρυφες λειτουργίες, στις χημικές ενώσεις που ξεφεύγουν το μάτι , ο φυσικοχημικός κόσμος και μαζί όλο το σύμπαν παρουσιάστηκαν σαν ένας μηχανισμός που τον ρυθμίζουν μερικοί απλοί και βασικοί νόμοι: η αδράνεια , η ανεξαρτησία των κινήσεων , ο νόμος της δράσης και της

αντίδρασης , που τους συμπλήρωσε ο νόμος της παγκόσμιας έλξης…….

Θεοδωρίδης

Οι Νευτώνειοι νόμου της κλασσικής μηχανικής παραδοσιακά θεωρούνταν, και θεωρητικά είναι, άπειρα ακριβείς στις προβλέψεις τους, δηλαδή σε προσέγγιση άπειρου πλήθους δεκαδικών ψηφίων, (στην πράξη είναι τόσο ακριβείς όσο η πειραματική τους επαλήθευση). ώστε να είναι δυνατός ένας έλεγχος μιας αυστηρής αιτιότητας στο σύστημα αυτό: στις ίδιες αιτίες αντιστοιχούν ίδια αποτελέσματα.

Στο Νευτώνειο σύστημα, το δόγμα της αιτιότητας διατυπώνεται ως εξής:

…Η εξέλιξη κάθε μηχανικού συστήματος ρυθμίζεται από αυστηρούς νόμους . Αυτοί σε συνδυασμό με την αρχική κατάσταση του συστήματος (το οποίο θεωρείται μεμονωμένο), καθορίζουν χωρίς αμφισημία όλες τις μελλοντικές καταστάσεις ακόμα και τις προηγούμενες.

Έτσι ολόκληρη η ιστορία του συστήματος κατά την εξέλιξη του χρόνου,

καθορίζεται από τους νόμους και από την αρχική του κατάσταση….Α. D’

Abro

Οι αυστηροί νόμοι είναι τα αξιώματα, οι νόμοι του Νεύτωνα, και η αρχική κατάσταση είναι οι προκείμενες του παραγωγικού συλλογισμού , οι θέσεις και οι ταχύτητες των σωμάτων του συστήματος.

Εδώ η αιτία του μηχανικού σύμπαντος μέσα στο παραπάνω σχήμα, είναι η δύναμη, και το αποτέλεσμα είναι η μεταβολή της κίνησης. Το σχήμα αυτό δεν περιλαμβάνει την αδρανειακή κίνηση, που είναι χωρίς αιτία, είναι φυσική αρχή. Οι αυστηροί νόμοι που αναφέρει ο d’ Abro είναι οι τρεις νόμοι του Νεύτωνα.

Ένα από τα μεγαλύτερα επιτεύγματα του Νεύτωνα είναι η ανακάλυψη της μεθόδου αναπαράστασης ενός φυσικού νόμου, και άρα μιας αιτιατής αλυσίδας, δια μέσου των μαθηματικών:

Είναι ο απειροστικός λογισμός όπου μιλούμε για στιγμιαία περιγραφή του φαινομένου της κίνησης, το πως λειτουργούν αίτιο και αποτέλεσμα σε μια στιγμή, ένα απειροστό διάστημα (κατά το διαφορικό λογισμό) για στιγμιαία ταχύτητα, για στιγμιαία επιτάχυνση, κι αυτό γιατί στη φύση όλα είναι μεταβαλλόμενα, η σταθερότητα είναι εξαίρεση^[2], η ταχύτητα ενός σώματος που πέφτει στη γη είναι μεταβαλλόμενη, η ταχύτητα των πλανητών γύρο από τον ήλιο είναι μεταβαλλόμενη κ.ο.κ., όμως σε ένα απειροστό χρονικό ή χωρικό διάστημα όλες οι μεταβολές «παγώνουν» η καμπύλη γίνεται ευθεία, οι δυνάμεις είναι σταθερές, η κίνηση είναι αδρανειακή κλπ. και έχουμε το απλό φαινόμενο της σύνθεσης σταθερών δυνάμεων με τον κανόνα του παραλληλογράμμου και τη σύνθεση των κινήσεων του Γαλιλαίου.

Έτσι η κίνηση κάθε στιγμής είναι η αιτία της κίνησης της επόμενης, αφού το φαινόμενο επαναλαμβάνεται με νέες τώρα αρχικές συνθήκες, αλλά με τον ίδιο νόμο. Η σελήνη λόγω αδράνειας θα κινούνταν κατά την εφαπτομένη της τροχιάς της προς το άπειρο. Όμως η βαρύτητα την έλκει προς τη γη , αλλά η αδράνεια δεν την αφήνει να πέσει πάνω στη γη. Η σύνθεση των δύο δυνάμεων κάθε χρονική στιγμή δίνει το τμήμα της τροχιάς την επόμενη στιγμή, ένα ατελείωτο μικροσκοπικό ζιγκ-ζακ. .

Η σχέση που συνιστά το νόμο προσεγγίζεται από μια οριακή διαδικασία, για να πετύχουμε το απειροστό χρονικό διάστημα της περιγραφής (D’ Abro). Για παράδειγμα , οι καταστάσεις ενός μηχανικού συστήματος , σε διαδοχικές στιγμές του

χρόνου t₀, t], t₂……….. t_n ορίζονται από τις θέσεις και τις ταχύτητες κατά τις στιγμές

αυτές. Ας υποθέσουμε ότι μελετούμε ένα σωματίδιο μάζας m στο οποίο ασκείται μια

δύναμη εξαρτώμενη από το χρόνο, κατά μήκος μιας ευθείας γραμμής. Αν είναι ρ και υ η θέση και η ταχύτητα του σωματιδίου τη χρονική στιγμή t, οι διαδοχικές καταστάσεις

ορίζονται (χο,υο) ,(χι, Ui)……… (Xn, Un)

Η σταθερή σχέση που συνδέει τη δύναμη με την επιτάχυνση είναι σε γενική

μορφή

Για να γίνει κατανοητή αυτή η νοητή διαδικασία, θα τη «δούμε» με το μικροσκόπιο, αποδίδοντας ένα κεφάλαιο απ’ το Principia του Νεύτωνα, όπου περιγράφεται η διαφορική αιτιότητα και η χρήση των νόμων του στην εξαγωγή ενός πραγματικού αποτελέσματος. Είναι το αντίστοιχο της μεθόδου της εξάντλησης στη γεωμετρία, ένα νοητικό πείραμα^[3] στην κίνηση.

Η πρόταση που αποδεικνύεται είναι ο γνωστός νόμος των εμβαδών του Κέπλερ, κατά την κεντρική κίνηση. Τώρα η προσπίπτουσα δύναμη μπορεί να είναι η βαρύτητα, και η κίνηση, η κίνηση της σελήνης γύρω από τη γη:

Τα εμβαδά που διαγράφει η επιβατική ακτίνα που συνδέει το κινητό με το ακίνητο κέντρο δύναμης, κείνται στο ίδιο επίπεδο και είναι ανάλογα με τους χρόνους διαγραφής τους . .( σχήμα 1)

Έστω ότι το πρώτο απειροστό χρονικό διάστημα το σώμα διαγράφει το τμήμα ΑΒ. Όποιου είδους κίνηση κι αν εκτελεί στο σύνολό της , πάντως στο απειροστό (πολύ μικρό) αυτό διάστημα η κίνηση μπορεί να θεωρηθεί αδρανειακή (με την Νευτώνεια έννοια). Όσο μικρότερο είναι το At (άρα και το κομμάτι της τροχιάς) τόσο πιο δικαιολογημένη είναι αυτή η ταύτιση. Αυτό θυμίζει το γεγονός ότι τα απειροστά τμήματα μιας καμπύλης είναι ευθύγραμμα.

Η αδρανειακή κίνηση του απειροστού τμήματος είναι το αμετάτροπο της τυχούσας κίνησης σε διεύθυνση και μέτρο. Το μέτρο της στην αρχή της κίνησης «εγγράφεται ανεξίτηλα» στο σώμα, το οποίο μπορεί να εκτελεί δύο κινήσεις (Γαλιλαίος) άρα και στις διαφορικές εξισώσεις κίνησης, με τη μορφή των αρχικών συνθηκών. Η θέση Α και η αδρανειακή του κίνηση (ταχύτητα) είναι οι αρχικές συνθήκες του συστήματος. Η κεντρομόλος δύναμη είναι η αιτία του φαινομένου.

Στο δεύτερο απειροστό τμήμα θα συνέβαινε το ίδιο . Αλλά μόλις το σώμα φτάσει στο Β υποθέτουμε ότι ασκείται σ’ αυτό μια κεντρομόλος                                                                                             δύναμη,

που το αναγκάζει να συνεχίσει την κίνησή του κατά το τμήμα BC, αντί της Bc. Φέρω τη cC παράλληλη της BS που συναντάει την BC στο C

Στο τέλος του δεύτερου απειροστού τμήματος του χρόνου το σώμα θα βρίσκεται στο C, στο ίδιο επίπεδο με το ASB.(Ευκλείδεια στερεομετρία)

To ίδιο θα συμβεί σε κάθε απειροστό τμήμα της τροχιάς με συνέπεια το κινητό να διαγράψει «διαδοχικά» τη γραμμή ABCDEF.

Εύκολα προκύπτει γεωμετρικά ότι το εμβαδόν SAB=SBC=SCD=SDE=SEF και με πρόσθεση π.χ τα SADS και SAFS έχουν μεταξύ τους την ίδια σχέση που έχουν οι χρόνοι που διαγράφηκαν.

Τώρα, αν το πλήθος των τριγώνων αυτών αυξηθεί, με το At άρα και τα ΑΒ, BC, κλπ να 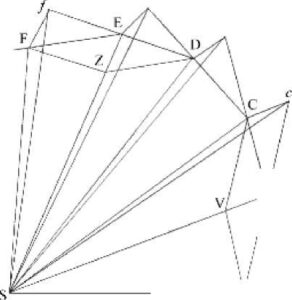τείνουν στο μηδέν (η λέξη τείνουν έχει ειδικό νόημα στο διαφορικό λογισμό) η τελική περίμετρος ABCDEF θα είναι μια καμπύλη και επίσης η

l κεντρομόλος δύναμη με την οποία το σώμα σύρεται διαδοχικά από την εφαπτομένη αυτής της καμπύλης θα δρα συνεχώς. Και οποιεσδήποτε διαγραφόμενες επιφάνειες θα είναι ομοεπίπεδες και ανάλογες των χρόνων διαγραφής.

Αυτή όλη η διαδικασία συντομεύεται με το διαφορικό φορμαλισμό (διαφορικές εξισώσεις) όπου παράγεται και το αποτέλεσμα: Η γωνιακή ορμή του κινητού ’■ .·, κατά την κεντρική κίνηση είναι σταθερή.

…. Η επιτυχία αυτών των υπολογισμών στην πρόβλεψη της

θέσεως ενός σώματος για μεγάλα χρονικά διαστήματα απετέλεσε τον θρίαμβο της αιτιοκρατίας. Η αιτιοκρατία και η προβλεψιμότητα^[4] θεωρήθηκαν έννοιες ταυτόσημες, εφόσον η εξέλιξη του φαινομένου διέπεται από καθαρά αιτιοκρατικούς νόμους, όπως είναι οι νόμοι του Νεύτωνα. Αυτό δημιούργησε την εικόνα, κυρίως κατά το δέκατο ένατο αιώνα και τις αρχές του εικοστού αιώνα, ενός καθαρά μηχανιστικού κόσμου, όπου τα πάντα είναι προβλέψιμα, με επιπτώσεις ακόμα και στη φιλοσοφική αντίληψη του κόσμου. (Χατζηδημητρίου)……………………….

Ο ντετερμινισμός της κβαντικής μηχανικής .

Μεγάλο μέρος της σύγχρονης αμφισβήτησης ή απλά συζήτησης γύρω από τον ντετερμινισμό παρουσιάζεται με επίκεντρο τα σύγχρονα πορίσματα της κβαντομηχανικής, όπου η δυνατότητα πρόβλεψης μειώνεται θεωρητικά, και όπου ένα πείραμα δεν είναι ποτέ επακριβώς επαναλήψιμο. Η κβαντική φυσική είναι η πιο ακριβής στις προβλέψεις της θεωρία, παράγει ακρίβεια υπολογισμών μέχρι δέκα πέντε δεκαδικά ψηφία ..αλλά αδυνατεί παραπάνω. Σύμφωνα με την ιδέα αυτού του άρθρου η αιτιοκρατία της φύσης υποχωρεί, έχουμε μειωμένη προβλεψιμότητα.

Σε λιγότερο από τρεις αιώνες μετά την τεράστια ανακάλυψη του Νεύτωνα , έχουν γεννηθεί αμφιβολίες για την εγκυρότητα των αυστηρά αιτιατών σχέσεων της κλασσικής μηχανικής. Η κρίση οφείλεται σε τελείως νέες ανακαλύψεις στον υποατομικό κόσμο, όπου παρατηρήθηκαν τα μυστηριώδη κβαντικά φαινόμενα.

Γνωρίζαμε μέχρι τότε την πρακτική αδυναμία του ελέγχου του δόγματος της αυστηρής αιτιότητας, δηλαδή θεωρητικά της άπειρης ακρίβειας της προβλεψιμότητας, η οποία οφείλεται στην αδυναμία μας να ενεργήσουμε σε τελείως μεμονωμένα συστήματα γιατί τέτοια συστήματα δεν υπάρχουν, ακόμα και γιατί η ανθρώπινη παρατήρηση είναι αναγκαστικά ανακριβής. Οι δυσκολίες αυτές δεν θεωρήθηκαν μοιραίες για το δόγμα, γιατί μπορούσαν να βρεθούν κατά προσέγγιση μεμονωμένα συστήματα και οι μετρήσεις μας μπορούσαν να βελτιωθούν τόσο ώστε να μην διαταράσσουν αισθητά τα υπό μέτρηση μεγέθη. Η κατάσταση εκφράζονταν με την άποψη ότι στην πράξη , η αυστηρή αιτιότητα δεν μπορούσε να ελεγχθεί, αλλά δεν υπήρχε θεωρητικό εμπόδιο στην πορεία για έναν αυστηρό έλεγχο. Η Νευτώνεια αιτιότητα έστειλε τον άνθρωπο στη σελήνη!

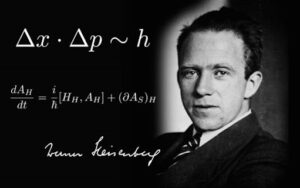
Η καινοτομία που προέκυψε από τις ανακαλύψεις της κβαντικής θεωρίας είναι ότι τώρα έχουμε λόγους να υποπτευόμαστε μια οριστική θεωρητική αδυναμία η οποία καθιστά μάταια κάθε προσπάθεια για αυστηρό έλεγχο των αιτιατών σχέσεων. Οι θεωρητικοί της κβαντικής θεωρίας , με επικεφαλής τους Χάιζεμπεργκ, Μπορν, Μπορ, και Ντιράκ, συμφωνούν με τους κλασσικούς επιστήμονες στο ότι οι πρακτικές δυσκολίες ελέγχου αυστηρών αιτιατών σχέσεων μπορούν να παραβλεφθούν. Αλλά είναι ανυποχώρητοι στον ισχυρισμό τους ότι οι θεωρητικές αδυναμίες που ανακαλύφτηκαν πρόσφατα, δεν μπορούν να αγνοηθούν εύκολα. Όπως μπορούμε να συμπεράνουμε από αυτή τη σύνοψη , η φιλοσοφία της κβαντικής φυσικής δεν προκύπτει από μια αναθεωρημένη ερμηνεία των κλασσικών γεγονότων, αλλά από την ανάγκη να συσχετίσουμε μια νέα κατηγορία γεγονότων για τα οποία δεν είχαμε καμιά υποψία στις προηγούμενες περιόδους .

Η εξέλιξη της κβαντικής θεωρίας δείχνει ότι οι ‘αρχές αβεβαιότητας’ που ανακαλύφτηκαν από το Χάιζεμπεργκ, και παρατηρήθηκαν πειραματικά, μας απαγορεύει κατ’ αρχήν να διενεργούμε συγχρόνως ακριβείς μετρήσεις για τα ονομαζόμενα συζυγή μεγέθη. Αυτή η πολύ γενική αρχή εφαρμόζεται ειδικότερα στη θέση και στην ταχύτητα, στο χρόνο και στην ενέργεια , στην ηλεκτρική και μαγνητική ένταση στο ίδιο σημείο του ηλεκτρομαγνητικού πεδίου. Έτσι αν η θέση του κέντρου ενός σωματιδίου μετρηθεί με ακρίβεια , η απρόβλεπτη διαταραχή που συνεπάγεται η ίδια η μέτρηση έχει ως αποτέλεσμα η ορμή του σωματιδίου να καθίσταται ασαφής. Ο κλασσικός ισχυρισμός ότι , με επαρκώς προσεκτικό πειραματισμό, μπορούμε να μειώνουμε τη διαταραχή επ’ άπειρον δεν ισχύει πια, γιατί η ουσία των αρχών της αβεβαιότητας είναι ότι το όριο στο οποίο ελπίζουμε να φτάσουμε δεν μηδενίζεται αλλά είναι πεπερασμένο. Προφανώς , αν γίνει αποδεκτή η αρχή αυτή, τότε η κατάσταση ενός μηχανικού συστήματος η οποία όπως γνωρίζουμε εμπλέκει μια ταυτόχρονη γνώση της θέσης και της ορμής των διαφόρων μαζών, δεν μπορεί να γίνει γνωστή . Συνεπώς ένας έλεγχος αυστηρής αιτιότητας είναι αδύνατος στη κβαντική μηχανική. Το ίδιο συμπέρασμα μπορεί να ισχύσει σε όλους τους τομείς της φυσικής. Μια αρχή που δεν μπορεί να ελεγχθεί ή ένα μέγεθος που δεν μπορεί να μετρηθεί κατ’ αρχήν, (όχι στην πράξη) θα πρέπει να πάψει να παίζει ρόλο στη θεωρητική συζήτηση. Το δίλημμα αυτό εμφανίστηκε και στη θεωρία της σχετικότητας όπου πρέπει να δεχτούμε ότι για λόγους που δεν έχουν σχέση με πρακτικές δυσκολίες του πειράματος , δεν μπορεί να διαπιστωθεί (να μετρηθεί) η ταχύτητα δια μέσου ενός ηρεμούντος αιθέρα. Η απόλυτη ταχύτητα έκτοτε αποπέμφθηκε από τη φυσική γιατί δεν μπορούσε να παρατηρηθεί κατ’αρχήν.

Πιο συγκεκριμένα, σε ατομικό επίπεδο, τα στοιχεία που περιγράφουν τις κινήσεις σωματιδίων μπορούν μόνο να υπολογιστούν πιθανολογικά. Η προέλευση αυτής της θεωρητικής αδυναμίας , απρόβλεπτης από την κλασσική επιστήμη , πρέπει να αναζητηθεί στην ίδια τη φύση των πραγμάτων. Είναι στενά συνδεδεμένη με τη σταθερά h του Πλανκ . Η θεωρητική αδυναμία θα εξαφανιζόταν αν η σταθερά αυτή , η τιμή της οποίας είναι πεπερασμένη, ήταν απειροστή όπως σιωπηρά είχε υποτεθεί από την κλασσική επιστήμη.

Οι κανονικότητες εδώ γίνονται αβεβαιότητες και ο λόγος που δεν τις βλέπουμε στην καθημερινότητα είναι ότι εμφανίζονται σε πολύ μικρή κλίμακα και γίνονται κυρίως εμφανείς στον μικρόκοσμο. Άρα το «σκληρό» ντετερμινιστικό μοντέλο δεν εφαρμόζεται παρά μόνο εάν θεωρήσουμε την πιθανολογική αβεβαιότητα μέρος της ντετερμινιστικής εικόνας για το Σύμπαν. Άλλωστε οι πιθανότητες είναι a priori, παραγόμενες από τις θεωρίες. Σε αυτή την περίπτωση όμως, η ιδέα πως το Σύμπαν δρα «όπως θα δρούσε ούτως ή άλλως» δεν ισχύει. Στην υποθετική περίπτωση που η ιστορία – ή μέρος της ιστορίας – θα επαναλαμβανόταν, η κβαντική αβεβαιότητα θα δημιουργούσε μια διαφορετική εκδοχή της ιστορίας.

Κι όμως το βασικό σχήμα της αξιωματικής μεθόδου φαίνεται κι εδώ να λειτουργεί. Η κρυμμένη κανονικότητα της επιβεβαίωσης των φαινόμενων από τη λογική εμφανίζεται τώρα με την εξίσωση του Schrodinger και τις πρώτες αρχές της κυματοσυνάρτησης , του πλάτους της κ.λ.π. Αυτό εκφράζεται από το Feynman: Μήπως αυτό σημαίνει ότι η φυσική , μια επιστήμη με τόση μεγάλη ακρίβεια, περιορίζεται στον υπολογισμό μόνο της πιθανότητας για την πραγματοποίηση ενός συμβάντος ,. ενώ αδυνατεί να προβλέψει με ακρίβεια τι πρόκειται να συμβεί; Η απάντηση είναι :Ναι! Αυτό αποτελεί μια υποχώρηση αλλά έτσι είναι τα πράγματα. Το μόνο που μας επιτρέπει η φύση , είναι να υπολογίζουμε πιθανότητες. Παρ’ όλα αυτά η επιστήμη δεν έχει καταρρεύσει όπως μας είχαν προειδοποιήσει οι φιλόσοφοι! R.

Feynman QED

Πράγματι με την αβεβαιότητα να «μολύνει» τα πειράματα και να διαλύει την αιτιότητα, φαίνονταν ότι όλα χάθηκαν. Δεν φαίνονταν δυνατό το πώς θα μπορούσε να υπάρξει μια επιστήμη του ορθού λόγου. Αλλά η κβαντομηχανική ανακάλυψε ακριβείς και κομψούς νόμους για να διαχειριστεί τις πιθανότητες, έτσι που η επιστήμη να ξεπεράσει τη δυσκολία της βασικής απροσδιοριστίας, η οποία είναι διαχειρίσιμη μαθηματικά.

…. Το μαθηματικό μέρος της κβαντικής θεωρίας υπαγορεύει τον

τρόπο που εξελίσσονται τα πλάτη των κυματοσυναρτήσεων ως προς το χρόνο. Η εξίσωση της εξέλιξης λέγεται εξίσωση Schrodinger ….με αυτόν τον τρόπο επιτυγχάνουμε μια περιγραφή του κόσμου που είναι βαθειά διαφορετική από την περιγραφή που παρέχεται από την κλασική φυσική , αλλά απολύτως συνεπής με αυτήν .Αν θέλετε να πείτε ότι η κβαντομηχανική είναι ντετερμινιστική , ναι είναι: η εξίσωση Schrodinger προβλέπει σαφώς την χρονική εξέλιξη των πλατών των πιθανοτήτων. Αν θέλετε να πείτε ότι η κβαντομηχανική είναι πιθανολογική , μπορείτε να το πείτε: οι μόνες προβλέψεις που δίνει αφορούν πιθανότητες ..David Ruelee Τύχη και χάος Τραυλός)

Επιστήμονες που αμφισβήτησαν την πιθανολογική εικόνα για το Σύμπαν προσπαθώντας να κρατήσουν την μέχρι τότε ντετερμινιστική (και αναζήτησαν την «κρυμμένη μεταβλητή») ήταν πολλοί. Ανάμεσά τους και ο Αϊνστάιν. Ο Αϊνστάιν και ο Πλανκ διατηρούν μια πίστη στην αυστηρή αιτιότητα, επεκτείνοντάς την μέχρι τη ζωντανή ύλη. Αλλά αυτοί που συνέβαλαν περισσότερο στην ανάπτυξη της νέας κβαντικής μηχανικής, απορρίπτουν τις απόψεις του Αϊνστάιν και ισχυρίζονται ότι η αυστηρή αιτιότητα είναι ένας μύθος.

Η πορεία του ντετερμινισμού, το χάος .

…Όμως εμφανίστηκε ρωγμή στην έννοια της κανονικότητας, και η συζήτηση για τον επιστημονικό ντετερμινισμό φούντωσε πάλι, με τη θεωρία του Χάους που ανιρνεύει τα όρια του αιτιατού και του τυχαίου.

Απλά αιτιοκρατικά συστήματα με λίγα μόνο στοιχεία μπορούν να γεννήσουν τυχαιότητα στη συμπεριφορά. Η τυχαιότητα αυτή είναι θεμελιώδης. Συλλέγοντας περισσότερες πληροφορίες δεν την εξαφανίζουμε. Η τυχαιότητα που γεννήθηκε με αυτόν τον τρόπο ονομάζεται χάος…^ϋϊ Lam (non linear systems for beginners)

Ο ντετερμινισμός αρκετά πρόσφατα, δέχτηκε τη μεγαλύτερη αμφισβήτηση. Υπάρχουν φαινόμενα που είναι απρόβλεπτα, δηλαδή η εξέλιξή τους δεν παρουσιάζει καμιά κανονικότητα. Τα φαινόμενα αυτά ονομάζονται χαοτικά. Τέτοια φαινόμενα είναι η τυρβώδης ροή ενός ρευστού, η κίνηση της μπάλας του μπιλιάρδου ή η εξέλιξη του καιρού, ακόμα και το ηλιακό μας σύστημα. Η θεωρία του χάους^{[5] [6]}, που θεωρείται ένα νέο άλμα της επιστήμης, έκανε απαγορευτική την πρόβλεψη ενός φαινομένου για μεγάλα χρονικά διαστήματα. Ειδικότερα, στο Ηλιακό σύστημα δεν μπορούμε να προβλέψουμε ποια θα είναι η θέση των πλανητών μετά από εκατό εκατομμύρια χρόνια⁶.(Χατζηδημητρίου) Και όμως, όλα αυτά τα φαινόμενα διέπονται από τούς ίδιους αιτιοκρατικούς νόμους του Νεύτωνα. Τότε γιατί η κίνηση δεν είναι στην περίπτωση αυτή κανονική και συνεπώς προβλέψιμη;

Η ιστορία του χάους είναι μια μαθηματική ιστορία και είναι μια ιδιότητα κάποιων λύσεων ενός συστήματος μη-γραμμικών εξισώσεων. Έχει τις αρχές της στο πρόβλημα των τριών σωμάτων και στις μελέτες του Πουανκαρέ, ο οποίος αποκάλυψε το χάος στο Ηλιακό σύστημα. Είχε κατανοήσει πως πολύ μικρές επιδράσεις μπορούν να μεγεθυνθούν μέσω ανάδρασης (επανάληψης). Διατύπωσε την άποψη “Μια ελάχιστη αιτία που διαφεύγει της προσοχής μπορεί να προκαλέσει ένα σημαντικό αποτέλεσμα”.

Ποιος αμφιβάλλει ότι η κίνηση του ζεύγους Γης-Σελήνης δεν επηρεάζεται από την έλξη του Ηλιου ή του Δία κλπ ; Το πρόβλημα είναι (και αυτό ακριβώς έθεσε ο

Πουανκαρέ) ότι κάνοντας το απλό βήμα από δύο σε τρία σώματα (προσπαθώντας για παράδειγμα να συμπεριλάβουμε τις επιδράσεις του Ηλίου στο σύστημα Γης- Σελήνης) οι εξισώσεις του Νεύτωνα, για τυπικούς μαθηματικούς λόγους, δεν επιλύονται: απαιτείται μια σειρά προσεγγίσεων για να «πλησιάσουμε» κάποια απάντηση ( οι σειρές που περιγράφουν τις τροχιές των τριών αλληλεπιδρώντων ουράνιων σωμάτων, όχι μόνο δεν συγκλίνουν σε κάποιες προκαθορισμένες θέσεις, αλλά αντίθετα αποκλίνουν!)^[7] .Αυτό καθιστά την επαναληπτικότητα βασικό χαρακτηριστικό των εξισώσεων του χάους. Για να λάβουμε τα δεδομένα σε μια χρονική περίοδο πρέπει η διαδιακασία να επαναληφθεί πολλές φορές οπότε το φαινόμενο ανατροφοδοτείται (ανάδραση). Κάθε προσέγγιση είναι μικρότερη της προηγούμενης και ο Πουανκαρέ ήλπιζε ότι μετά από ένα δυνητικά άπειρο αριθμό τέτοιων διορθώσεων να φτάσει στη σωστή απάντηση. Όμως το αποτέλεσμα ήταν συγκλονιστικό! Υπήρχαν μερικές τροχιές, για τις οποίες μια μικρή βαρυτική έλξη από κάποιο τρίτο σώμα θα μπορούσε να αποσυντονίσει την κίνηση του πλανήτη , ακόμα και να τον πετάξει έξω από το πλανητικό σύστημα.(ο ταραγμένος καθρέπτης σελ. 29)

…. Ο Πουανκαρέ αποκάλυψε ότι το χάος , ή η δυνατότητα

δημιουργίας χάους , είναι η ουσία ενός μη γραμμικού συστήματος και πως ακόμα και ένα πλήρως προσδιορισμένο σύστημα , όπως οι περιστρεφόμενοι πλανήτες , θα μπορούσε να έχει απροσδιόριστη εξέλιξη. Από μια άποψη είχε κατανοήσει τον τρόπο με τον οποίο πολύ μικρές επιδράσεις θα μπορούσαν να μεγεθυνθούν μέσω της ανάδρασης⁸. Είχε διακρίνει πως ένα απλό σύστημα μπορεί να καταλήξει

σε ανεξέλεγκτη και εντυπωσιακά περίπλοκη συμπεριφορά ……………… ο

ταραγμένος καθρέφτης

Με το θόρυβο για την κβαντική θεωρία και τη σχετικότητα , η ανακάλυψή του έπεσε στην αφάνεια. Ακόμη και ο ίδιος τα είχε εγκαταλείψει λέγοντας «αυτά τα πράγματα είναι τόσο αλλόκοτα που δεν αντέχω να τα αντικρύσω»

Μόλις τη δεκαετία του 1960 οι έρευνές του συνδυάστηκαν με νέες εργασίες σε μια νέα επιστήμη του χάους και της μεταβολής, και έχουν οδηγήσει σε νέες αντιλήψεις προς την κατεύθυνση της ολότητας της φύσης μακριά από το στεγνό κυρίαρχο μοντέλο του αναγωγισμού (η αντίληψη ότι ο κόσμος αποτελεί συνάθροιση μερών) και της γραμμικότητας (όπου η σχέση αιτίας και αποτελέσματος είναι γραμμική, δηλαδή μια σχέση όπου σε διπλάσια αιτία αντιστοιχεί διπλάσιο αποτέλεσμα κ.ο.κ., όπως π.χ. με τη δύναμη που ασκεί ένα ελατήριο, όπου σε διπλάσια επιμήκυνση έχουμε διπλάσια δύναμη)..

Μη γραμμικά συστήματα

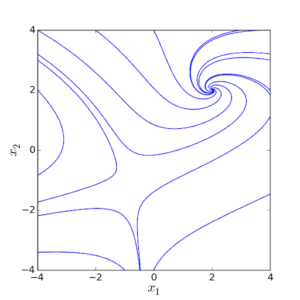Σήμερα γνωρίζουμε ότι όλα τα δυναμικά συστήματα (συστήματα σωμάτων που αλληλεπιδρούν μεταξύ τους και η θέση τους εξελίσσεται στο χρόνο), από τους πλανήτες μέχρι τις αέριες μάζες στην ατμόσφαιρα και τον καπνό του τσιγάρου που στροβιλίζεται, είναι μη γραμμικά (η σχέση αιτίας και αποτελέσματος είναι μη- γραμμική). H συμπεριφορά των μη γραμμικών συστημάτων μπορεί να διαφέρει ποιοτικά από αυτήν των γραμμικών και δεν μπορούμε να χρησιμοποιήσουμε τις λύσεις γραμμικών εξισώσεων σαν οδηγό για την κατανόηση της συμπεριφοράς πολλών συστημάτων του πραγματικού κόσμου.

Τα μη γραμμικά συστήματα μπορούν να επιδείξουν μια ποικιλία συμπεριφορών , συμπεριλαμβανομένου του χάους. Αυτό έχει βαθιές συνέπειες σε όλες τις επιστήμες. Επίσης έχει αλλάξει την άποψή μας ως προς την αρχή του επιστημονικού ντετερμινισμού. Η φύση είναι εσωτερικά μη γραμμική και η μη- γραμμικότητα είναι ο κανόνας παρά η εξαίρεση.

..η Βίβλος δεν μας λέει ότι οι νόμοι της φύσης εκφράζονται γραμμικά        Enrico Fermi

Χρησιμοποιώντας τον όρο μη-γραμμική επιστήμη είναι σαν να

αποκαλούμε τη ζωολογία ως τη μελέτη των μη-ελεφάντων….. Stanislaw

Ulam

Η μακροχρόνια μελέτη των γραμμικών συστημάτων, παρ’ όλο που αποτελούν εξαίρεση, οφείλεται στο ότι όλα τα γραμμικά προβλήματα είναι επιλύσιμα, ενώ τα μη γραμμικά σπάνια επιλύονται επακριβώς. Πριν την έλευση των υπολογιστών , σχεδόν τίποτα δεν μπορούσαμε να συμπεράνουμε για τη μη-γραμμική συμπεριφορά. Ακόμα πολλά μη γραμμικά συστήματα είναι κατά προσέγγιση γραμμικά

Σε ένα γραμμικό μαθηματικό σύστημα μπορούμε να συνδυάσουμε δύο λύσεις και το αποτέλεσμα να είναι λύση του συστήματος, (αναγωγισμός). Τα μη- γραμμικά συστήματα όμως δεν μπορεί να συμβεί αυτό. Θα πρέπει να διαπραγματευτούμε μαζύ τους, σε όλη τους την περιπλοκή, και περιγράφονται από μη γραμμικές διαφορικές εξισώσεις , (που είναι οι αντίστοιχες των γραμμικών εξισώσεων του Νεύτωνα (που θεμελίωσαν τον μηχανοκρατικό ντετερμινισμό) οι οποίες άργησαν να μελετηθούν,( το 19^ο αιώνα οι μαθηματικοί δεν τις γνώριζαν επαρκώς, απλά χρησιμοποιούσαν γραμμικές προσεγγίσεις τους), είναι ευσταθή για το μεγαλύτερο διάστημα της ζωής τους και δεν είναι δυνατόν να διαιρεθούν στα μέρη τους , η παραμικρή επίδραση μπορεί να προκαλέσει εκρηκτική αλλαγή, και ξαφνικά οι επιστήμονες συνειδητοποίησαν πως σε αιτιοκρατικά δυναμικά συστήματα, η δυνατότητα γέννησης χάους (μη προβλεψιμότητας) παραμονεύει σε κάθε λεπτομέρεια.

Ένα μοντέλο χαοτικής συμπεριφοράς, επαναληπτικές συναρτήσεις

Το Χάος δεν σχετίζεται κατ’ ανάγκη με περίπλοκα συστήματα και αφηρημένες έννοιες.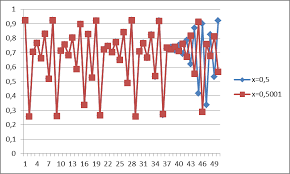 Μπορούμε να βρούμε χαοτική συμπεριφορά και σε απλά συστήματα και έτσι να μελετήσουμε το απροσδιόριστο, στη πιο βασική του μορφή. Ακόμα και στις πιο απλές εξισώσεις δευτέρου βαθμού έχουμε χάος, αρκεί να τις χειριστούμε σαν δυναμικά συστήματα. Αυτό το επιτυγχάνουμε αν τις χειριστούμε σαν επαναληπτικές συναρτήσεις, δηλ. αν έχουμε κάθε τόσο ανατροφοδότηση της τιμής της από το αμέσως προηγούμενο αποτέλεσμα (συνεχής σύνθεση της συνάρτησης με τον εαυτό της).(Αναστασία Καρακώστα)

Η δευτεροβάθμια y=r x(1-x) θα μας δώσει όλες τις μαθηματικές ιδιότητες του χάους , όταν μεταφραστεί σε ένα δημογραφικό μοντέλο που δημοσιεύτηκε από τον βιολόγο Robert May στα πρότυπα του μοντέλου του Velhulst^[8]. Λέγεται λογιστική απεικόνιση, όπου η επαναληπτικότητα χειρισμού της παίρνει τη μορφή

Χν+1 =Ρ Χν (1-Χν) ………… (1)

όπου χ_ν είναι ο αριθμός του πληθυσμού την περίοδο ν και χ_ν+₁ ο πληθυσμός την επόμενη περίοδο (έτος , δεκαετία κλπ) .

Το ρ>0 είναι η παράμετρος αναλογίας που εκφράζει το ρυθμό γεννήσεων .

Η (1) είναι ένα πρωτότυπο μιας μη-γραμμικής επαναλαμβανόμενης διαδικασίας όπου υπολογίζουμε την εξέλιξη ενός πληθυσμού, αρχίζοντας με κάποια αρχική τιμή του πληθυσμού χ₀ (μεταξύ του 0 και 1) και εφαρμόζοντας τον τύπο ξανά και ξανά επιτυγχάνοντας διαδοχικά μια ακολουθία τιμών χ₁, χ₂, χ₃,….κλπ^[9]. Όταν αναπτύξουμε αυτό το επαναληπτικό σχήμα θα βρούμε ότι το αποτέλεσμα στην εξέλιξη του πληθυσμού εξαρτάται σε μεγάλο βαθμό , από την τιμή του ρ (εκθετική απομάκρυνση). Επίσης η εξέλιξη είναι πολύ ευαίσθητη στην αρχική τιμή του πληθυσμού χ₀. Ακόμα και μια απόκλιση ας πούμε κατά χιλιοστό δεκαδικό ψηφίο στην τιμή του χ₀ θα έχουμε μια σημαντική διαφορά στο τελικό αποτέλεσμα σε μια τελείως διαφορετική εξέλιξη. Αξίζει να σημειώσουμε ότι ακόμα και οι υπολογιστές μας που «δουλεύουν» με ακρίβεια ενός σταθερού αριθμού δεκαδικών, υπόκεινται σε αυτού του είδους την αδυναμία της προβλεψιμότητας οσοδήποτε ισχυροί κι αν είναι ¹¹(Marcel Ausloos, Michel Dirickx)

Τι παρατηρούμε για την εξέλιξη αυτού του δυναμικού μη-γραμμικού συστήματος της εξέλιξης του πληθυσμού σε ένα μεγάλο χρονικό διάστημα; Δηλαδή τι

μαθηματικά αποτελέσματα έχουμε για την ακολουθία χ₁, χ₂,                  χ₃ ………. των τιμών

του πληθυσμού, που παράγονται από την επανάληψη της (1);

1 .για ρ<1 η ακολουθία του πληθυσμού τείνει στο 0, ανεξάρτητα από την τιμή του ρ. Αυτό είναι εύλογο αφού οι θάνατοι είναι περισσότεροι από τις γεννήσεις, ο πληθυσμός θα αφανιστεί.

2. για 1<ρ<3 η ακολουθία του πληθυσμού τείνει στο 1. για ρ<2 αυτό συμβαίνει κατά ένα μονότονο τρόπο αλλά για 2<ρ<3 γίνεται με μια ταλάντωση των τιμών. Ο πληθυσμός παίρνει μια ελάχιστη και μια μέγιστη τιμή! Καθώς το ρ αυξάνεται στο 3 οι ταλαντώσεις επίσης αυξάνονται σε πλάτος και μήκος.
3. για 3<ρ< 3,5699 η ακολουθία γίνεται περιοδική με περίοδο που εξαρτάται από το ρ¹². Πρώτα έχουμε μια ταλάντωση με περίοδο 2 (μέγιστο και ελάχιστο) μετά μια ταλάντωση του πληθυσμού ανάμεσα σε 4 τοπικά ακρότατα (περίοδος 4) και στη συνέχεια , καθώς αυξάνει το ρ, περίοδο 8, 16 κοκ. Τώρα το σύστημα ετοιμάζεται για χαοτική συμπεριφορά, δεν μπορούμε να διακρίνουμε οποιαδήποτε τάξη στον αυξανόμενο και μειούμενο αριθμό του πληθυσμού. Οι τιμές του πληθυσμού θα γίνουν απρόβλεπτες δηλαδή ανεξήγητες αιτιατά.
4. για τιμές 3,5699<ρ< 4 το σύστημα γίνεται χαοτικό , το μέγεθος του πληθυσμού σε κάθε βήμα της επανάληψης θα είναι διαφορετικό από την τιμή του σε οποιοδήποτε από τα προηγούμενα βήματα. Δεν υπάρχει πλέον σταθερότητα ούτε κανονικότητα.!

Ντετερμινισμός και χάος

• Logistic map and the route to chaos Marcel Ausloos, Michel Dirickx
• Περιοδική ακολουθία με περίοδο p είναι όταν ισχύει a_n+_p=a_n για κάθε n

Έτσι που συνδέσαμε τον ντετερμινισμό με την προβλεψιμότητα, οι χαοτικές συμπεριφορές είναι μη προβλέψιμες άρα μη ντετερμινιστικές . Όμως

…. Στην πραγματικότητα η κίνηση είναι πάντοτε αιτιοκρατική,

δηλαδή στην ίδια αρχική κατάσταση αντιστοιχεί πάντοτε η ίδια τελική κατάσταση. Αν ήμασταν σε θέση να γνωρίζουμε ακριβώς την αρχική κατάσταση με απέραντη ακρίβεια και επιπλέον αν ήμασταν σε θέση να εκτελέσουμε τους αριθμητικούς υπολογισμούς με απόλυτη ακρίβεια (χωρίς να στρογγυλεύουμε το αριθμητικό αποτέλεσμα, π.χ. στο 20ό δεκαδικό ψηφίο), τότε δεν θα είχαμε κανένα πρόβλημα στην πρόβλεψη ενός φαινομένου και δεν θα κάναμε διάκριση μεταξύ κανονικών και χαοτικών κινήσεων. Ποτέ όμως δεν είναι δυνατόν να κάνουμε μετρήσεις, με απόλυτη ακρίβεια, π.χ. της θέσης και της ταχύτητας ενός σώματος, με

13

απόλυτη ακρίβεια….. (Χατζηδημητριου)

Η άποψη αυτή του καθηγητή Χατζηδημητρίου αναφέρεται στην αιτιότητα καθ’

εαυτήν, αφού τελικά…….. δεν μπορούμε να κάνουμε προβλέψεις. Αν δύο χύτρες με

σούπα θερμανθούν υπό τις ίδιες ακριβώς συνθήκες θα συμπεριφερθούν διαφορετικά. Οι συνθήκες στα δυναμικά συστήματα ουδέποτε είναι πανομοιότηπες αλλά συνήθως τις αγνοούμε επειδή δεν μεγεθύνονται μετατρέποντας το συνηθισμένο σε χαοτικό. Αυτό συμβαίνει σε συνθήκες ανάδρασης. Φαίνεται σαν κάποια στιγμή «χάνεται» η σχέση μεταξύ αιτίας και αποτελέσματος! Στα χαοτικά συστήματα δε υφίσταται ο εκτελεστικός ντετερμινισμός που αναλύσαμε.

Με αυτή τη σχέση ο επιστημονικός ντετερμινισμός απεικονίζεται με το σχήμα :

Γραμμικά συστήματα + αξιώματα Νεύτωνα — αυστηρός ντετερμινισμός Νευτώνειος ντετερμινισμός +αρχές αβεβαιότητας — αβεβαιότητα μη γραμμικά συστήματα+ επανάληψη —— τυχαιότητα

πηγές .

Η Αριστοτελική κίνηση στη σύγχρονη φυσική www mpantes. gr Mathematics and the physical world, Morris Klein, Dover Χώρος και σχετικότητα, Φρανσουάζ Μπαλιμπάρ, Εστία H ελαφρότητα του είναι, Frank Wilczek (Κάτοπτρο)

The rise of the new physics A.D’ Abro (Dover)

Εισαγωγή εις την κβαντομηχανικήν Γ.Ι. Ανδριτσόπουλος

¹³ Ο καθηγητής Χατζηδημητρίου ήταν ένας ξεχωριστός δάσκαλός μου στο Πανεπιστήμιο της Θεσσαλονίκης που με μύησε στα μυστικά της Νευτώνειας φυσικής.

Η Κβάντωση του χώρου και του χρόνου (άρθρο, mpantes on scribd)

Ο ταραγμένος καθρέφτης Gohn Briggs , F. David Peat ΚΑΤΟΠΤΡΟ ΧΑΟΣ ΣΤΟ ΗΛΙΑΚΟ ΣΥΣΤΗΜΑ Ιωάννης Δ. Χατζηδημητρίου (διαδίκτυο) Logistic map and the route to chaos: Marcel Ausloos, Michel Dirickx Α primer on Determinism Door John Earman (klwver the language of science) Great Physicists from Galileo to Einstein George Gamow (Dover)

Τύχη και χάος David Ruelle (Τραυλός)

Γνωριμία με τα φράκταλς Διπλωματική εργασία Αναστασία Καρακώστα

QED R.Feynman Tροχαλία

Non linear systems for beginners, Lui Lam

² Αργότερα θα καταλάβουμε ότι όλα στα φύση είναι μη γραμμικά (θεωρία του χάους) , η Νευτώνεια γραμμικότητα είναι εξαίρεση, έτσι συνεχώς με εμβάθυνση των κανονικοτήτων προχωράει η επιστήμη.

^[1] Είναι εκπληκτικό το.. εύρος της διερεύνησης ύστερα από 25 αιώνες : στην προσπάθεια των φιλοσόφων να ορίσουν την έννοια της αιτιότητας καθεαυτής, εμφανίστηκαν πολλές εργασίες (αιτιώδης ρεμπουπλικανισμός (causal republicanism») με την άποψη ότι «παρ’ όλο που η έννοια της αιτιότητας είναι χρήσιμη, ίσως απαραίτητη στις επαφές μας με τη φύση είναι μια κατηγορία που δεν μας δόθηκε ούτε από Θεό ούτε από τη φύση , αλλά μάλλον κατασκευάστηκε από εμάς, Steven Weinstein Causality and relativity». Αυτός οι αιτιώδης ρεπουμπλικανισμός βρίσκεται στα Αναλυτικά Υστερα του Αριστοτέλη τον 4^ο αιώνα π.Χ

…«Με τους διαφορικούς νόμους, η κινητική κατάσταση ενός συστήματος σε δεδομένη χρονική στιγμή παράγει την κινητική του κατάσταση σε μια αμέσως επόμενη στιγμή .πριν το Νεύτωνα δεν υπήρχε κανένα πλήρες σύστημα για τη φυσική αιτιότητα, η ιδέα πως υπάρχει μια ακλόνητη φυσική αιτιότητα δεν μπορούσε να στηριχτεί σε κανένα απτό αποτέλεσμα. Μόνο οι διαφορικοί νόμοι είναι σε θέση να ικανοποιήσουν τις απαιτήσεις αιτιότητας                        της μοντέρνας

φυσικής…… Einstein

Αν θέλουμε να γνωρίσουμε καταστάσεις του συστήματος ύστερα από ένα πεπερασμένο διάστημα του χρόνου , θα πρέπει να επαναλάβουμε την προηγούμενη διαδικασία στις άπειρες διαδοχικές χρονικές στιγμές. Η δυσκολία ξεπερνιέται με την ανακάλυψη από το Νεύτωνα της μεθόδου ολοκληρώσεως. Χάρις σ’ αυτήν τη μαθηματική μέθοδο είναι πάντοτε δυνατόν, τουλάχιστον θεωρητικά, να ακολουθήσουμε την αιτιατή αλυσίδα πάνω σε πεπερασμένα χρονικά διαστήματα.

Ο νοητός ‘μηχανισμός’ της διαφορικής αιτιότητας .

^[3] Τα νοητικά πειράματα εισήχθησαν από το Γαλιλαίο, εγκαταλείφθηκαν από την επιστήμη το 18^ο και 19^ο αιώνα και επανήλθαν με τον Αϊνστάιν.

^[4] Η δυνατότητα για ένα προβλέψιμο σύμπαν έφτασε στο απόγειό της με το μηχανικό σύμπαν του Νεύτωνα., αν και ο Νεύτων καθώς και ο Λαπλάς την αμφισβήτησαν. Ο πρώτος γιατί γνώριζε τα σφάλματα των αστρονομικών παρατηρήσεων και ο δεύτερος πιο θεωρητικά, επινόησε ένα σούπερ σοφό ον, σε αντίθεση με τα πεπερασμένα μυαλά των ανθρώπων, τα οποία θα παραμένουν σε άπειρη απόσταση από τη γνώση . Γνώριζε καλά ότι η πληροφορία και για ένα απλό σωματίδιο είναι απείρως μαθηματική.

^[5]          Η ονομασία Θεωρία του Χάους δόθηκε από τον μαθηματικό του Πανεπιστημίου του Maryland Jim York μόλις το 1975

^[6] Το διάστημα αυτό μπορεί να φαίνεται πολύ μεγάλο για την καθημερινή ζωή, σε αστρονομική κλίμακα όμως είναι μικρό. Πράγματι, σε σχέση με την ηλικία του Ηλιακού συστήματος (4.6 δισεκατομμύρια χρόνια), είναι περίπου τα δύο εκατοστά της ηλικίας του.

^[7] Ο Abel έλεγε ότι οι αποκλίνουσες σειρές είναι όργανα του διαβόλου.

^[8] Το μοντέλο του Velhulst εφαρμόστηκε επίσης στην κοινωνιολογία και στα οικονομικά και εντελώς ξαφνικά, απέκτησε μεγάλη σπουδαιότητα γιατί συνδέθηκε με τη θεωρία του χάους, πράγμα που ο ίδιος ποτέ δεν το είχε φανταστεί.

^[9]  Όλα τα μη-γραμμικά συστήματα έχουν παρόμοια ιδέα στη χαοτική διερεύνηση.